QuiproquoDernière mise à jours 2024-05-05 par Mathilde Ohm |
Octobre (semaine 40)
Il y a deux semaines, j’avais noté qu’à l’expression « Je ne sais pas,.. »,
Nous avons commencé l’étude du trinôme du second degré : La forme canonique, la factorisation et le réputé discriminant , tout y passe ! Il y a même un autre nom pour ce sujet : La parabole. Ce doit être un sujet important parce qu’on en parle en physique, en français et en mathématiques. Le second degré, ici, ce n’est pas de l’humour et franchement je ne vois pas pourquoi le même nom parabole est le nom d’une forme physique et une figure de rhétorique.
 |
 |
 |
Je suis intriguée aussi par l’utilisation du terme de « forme canonique » pour caractériser l’expression
 |
Ce n’est tout de même pas parce que le boulet décrit une parabole ! Il semble bien que ce soit plus proche de l’idée d’une forme de la langue qui répond aux normes les plus habituelles de la grammaire. Si j’ai bien compris, sont canoniques certaines notions traditionnellement estimées fondatrices. J’y rangerais bien le théorème de Pythagore, celui de Thalès |
 |
Il semble que
Cette semaine, le prof nous a soumis un petit exercice : , expression pour laquelle on cherche la (ou les) valeur(s) de
qui vérifie(nt) l’égalité. Quand je relis ce travail que j’ai placé page suivante, je vois comme il est facile de se laisser tromper par une lecture rapide : après avoir élevé au carré les deux membres de l’égalité, on résout un trinôme du second degré dont le discriminant est strictement positif ; il y a donc deux solutions
ou
.
Mais, là, patatras. Il convenait de limiter le domaine de définition à La réponse
est une solution qu’on ne peut pas accepter parce
et
avec
sont égaux entre eux et égalent
et donc n’ont pas d’existence réelle. Lorsque les calculs sont embrouillés (par des expressions longues, par exemple) le domaine de définition ne devient explicite qu’au moment de la synthèse. La question sous-jacente est donc celle des implications et c’est là que la question « Pourquoi écrire
, puisqu’il n’y a qu’une réponse ? » montre sa pertinence. L’expression
se comprend quand on la rapporte aux implications, aux relations et non pas aux solutions !
L’exercice supposait que j’avais bien intégré la définition des nombres réels. Et je pense avoir bien compris le cours de seconde concernant les ensembles.
En fait, cela n’est pas si évident. Savoir placer un nombre dans le bon ensemble ne suffit pas. Encore faut-il, le cas échéant, penser à vérifier que la solution trouvée soit dans le bon ensemble. Pour le dire autrement, connaître le sens d’un mot c’est savoir s’en servir. La signification des l’adjectifs « entier », « naturel », « relatif » … consiste aussi à définir la signification par l’usage, par les procédures qu’ils mettent en jeu.
Cela s’illustre encore dans mon interrogation de cours :

Cette discussion avec moi-même s’origine dans mes remarques, mes observations et même les corrections de mes erreurs. C’est dire l’importance d’en faire part. Tout cela ne tombe pas sous le sens — n’est pas évident — et ne va pas sans dire ! — et mérite d’y réfléchir. Je me félicite encore de profiter de l’occasion de préciser mes idées.
Et pour en dire un peu plus :
Penser n’est pas sortir de la caverne,
ni remplacer l’incertitude des ombres par les contours tranchés des choses mêmes,
la lueur vacillante d’une flamme par la lumière du vrai Soleil.
C’est entrer dans le labyrinthe, plus exactement faire être et apparaître un Labyrinthe
alors que l’on aurait pu rester « étendu parmi les fleurs, faisant face au ciel ».
C’est se perdre dans des galeries qui n’existent que parce que nous les creusons inlassablement,
tourner en rond au fond d’un cul-de-sac dont l’accès s’est refermé derrière nos pas –
jusqu’à ce que cette rotation ouvre, inexplicablement, des fissures praticables dans la paroi.
Castoriadis (C.), Les carrefours du labyrinthe, I, Seuil, Paris, 1998, p. 6.

Les freins à la compréhension. De même que le sens du mot que l’on a commencé à lire est anticipé dès les premières lettres de celui-ci, le sens de la phrase le sera dès la lecture de ses premiers mots, chaque anticipation étant susceptible d’être corrigée au fur et à mesure de la progression de cette lecture. Le phénomène renvoie en cela à la circularité du tout et des parties. « Les opposés des opposés sont des opposés », ou : « ce qui appartient à la partie appartient au tout » ? Mais peuvent-ils inclure aussi des jugements de valeurs, donc des comparaisons comme « une chose bonne, c’est adopter un bien plus grand au lieu d’un moindre bien et, entre deux maux, de choisir le moindre » ? La question disparaît quand la réponse est obtenue. Nous avons des préjugés. On lit, on écoute, on regarde avec nos préjugés. Le lecteur invente l’histoire. Est-ce possible en math ? La vidéo ci-dessous à une durée inférieure à deux minutes.
Si je regarde mon cours sur mathenpoche.sesamath.net je vois : La somme Il n’y a pas beaucoup de différence et je continue de penser que ma réponse est sans erreur. D’ailleurs, la correction en rouge dit que je n’ai pas répondu à la question, pas que j’ai écrit une erreur. En fait, dans ma précipitation, j’ ai bien observé que la suite était géométrique, donc de raison Quantificateurs : Les quantificateurs universel Non. Ce n’est pas la correction de mon erreur, puisqu’absent, les quantificateurs n’étaient pas mal positionnés. ! En revanche, voilà ma question je pensais : Je ne peux pas mettre pour tout Mon père dit « Méfie-toi de ne pas te perdre dans les détails, ne jette pas le bébé avec l’eau du bain. ». Comment mettre de l’ordre dans tout ce fatras ? Que retenir de ces quelques exercices ? Au total, cette semaine, et plus spécialement cet exercice, m’a rappelé l’utilité du doute, et la nécessité d’en revenir aux textes, que ce soit Pythagore, Thalès, comme au collège, ou les formules de calcul, cette fois c’était la somme des termes. Je complète donc ma carte pour mémoriser tout cela. |


 En vérifiant, je découvre que le prof attendait :
En vérifiant, je découvre que le prof attendait : Un peu plus loin, dans ma copie, le signe d’équivalence est barré puis remplacé par le digne égal.
Un peu plus loin, dans ma copie, le signe d’équivalence est barré puis remplacé par le digne égal.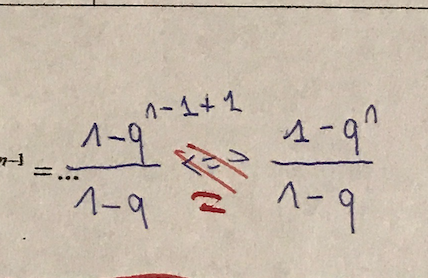 Il m’a fallu un peu de temps pour distinguer les signes
Il m’a fallu un peu de temps pour distinguer les signes  parce que la ligne : (Pour tout
parce que la ligne : (Pour tout 