Jeudi nous avons préparé le cours de fin de semaine du lycée. 

Tout d’abord pour se remémorer les prérequis et reconstituer le contexte dans lequel se situe le deuxième épisode de la série « dérivation ».  

Être dispensé, pendant l’exposé scolaire, des efforts de mémoire, facilite l’observation des détails du cours présenté. 

D’autre part, cela conduit à mesurer l’écart entre ce que l’on prévoit et ce qui est effectivement enseigné. 

 

Samedi la cohérence partielle entre la préparation et l’exposé était établie. 

 

C’est « l’essentiel » qui a été décortiqué. Certains détails sont pertinents, d’autres sont négligeables. Faire le tri aide à se dégager des éléments encombrants : 

 

 

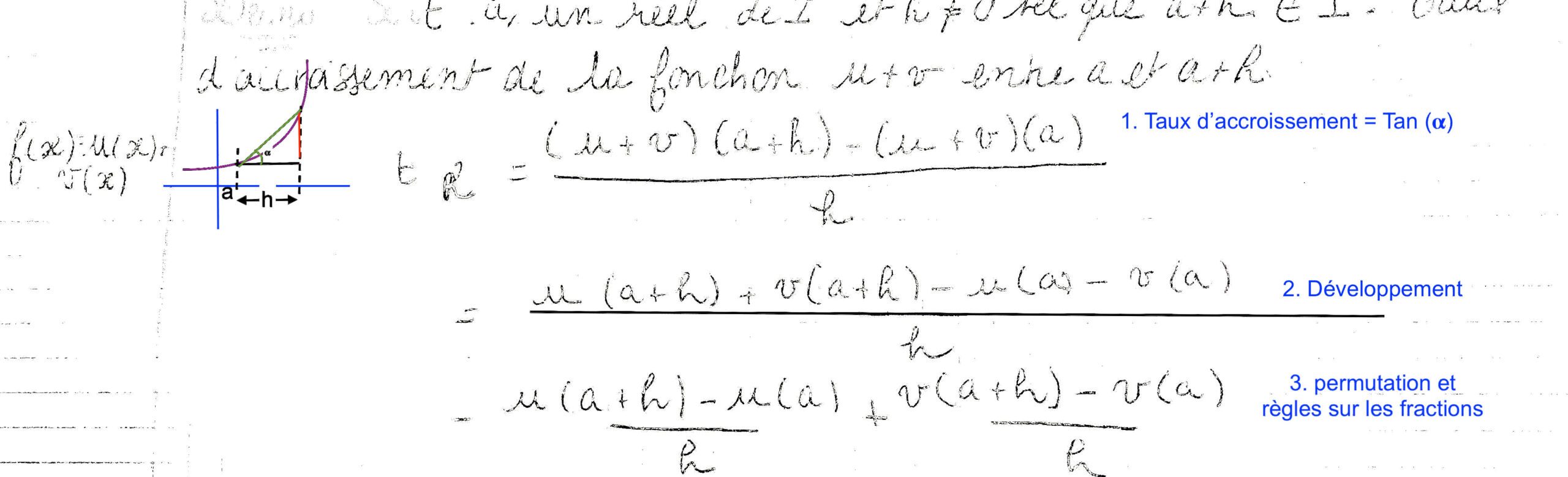
De même, faire émerger de :

 

*** QuickLaTeX cannot compile formula :
\mathbf ​​(uv)' = u'v + uv'

*** Error message :
Invalid UTF-8 byte sequence (✥group\else).
leading text: $\mathbf ⍊

   et que cela se démontre aisément en développant le produit 

pour en faire une somme et revenir à la question précédente. 

 

Parce qu’on a compris où se trouve l’essentiel, on réalise que le travail est fait. 

Voilà ce qu’en dit Alain Connes médaille Field : 

 

Se résume de façon lapidaire ​ :  

 

Dégager l’essentiel d’un texte, fut-il mathématiques, est un acte volontaire et conscient, 

du moins pendant la phase d’apprentissage.