Proto épreuve

Qu'en penser ? Dernière mise à jours 2024-04-05 par Mathilde Ohm

Touches voisines

Octobre (semaine 41)

J’ai parfois l’impression que l’horizon recule au fur et à mesure que j’avance et que les mathématiques sont sans limite. Beaucoup de gens se rangent à l’idée commune qu’en mathématiques les mots ont un seul sens.
Et jusqu’en ,  « tangente » était  le nom  d’une ligne droite qui caresse un cercle sans le percer. Au point de ce cercle,   c’est la droite passant par   perpendiculaire au rayon …

… en classe de troisième, le mot  « tangente »  de l’angle désignait, alors, dans un triangle rectangle en ,   le rapport du  côté opposé à   au  côté adjacent à  : . Pourquoi donc utiliser un même mot pour deux choses différente ? Heureusement, pour m’aider à me souvenir, j’ai retenu que c’est le nombre , affiché sur le panneau du code de la route,  qui  indique la mesure de la pente qui s’élève de 7 mètres pour 100 mètres. Cependant le panneau  me paraît ambigu et j’ai longtemps hésité à me  rapporter  au déplacement horizontal plutôt que sur la route elle-même,  en oblique ?

milieu (du cercle, d’un segment).

rayon,

premier (nombre premier et premier nombre) ,
encadrer (une valeur, un résultat),
degré (d’un polynôme et mesure d’un angle),
racine (du polynôme, du carré),

0…9 ( en tant que nombres ou que chiffres).

…

Ma grand-mère m’a appris très tôt comment cueillir les étoiles : la nuit, il suffit de poser une bassine d’eau au milieu de la cour pour les avoir à ses pieds.
Le Ventre de l’Atlantique (2003). Fatou Diome (1968- )

Il me semble que ma carte de mémorisation est un peu comme cette bassine et que je commence à décrocher quelques bonnes étoiles et notamment ce point d’étude qu’est le nombre dérivé qui ne laisse pas capter du premier coup d’œil.

En classe, j’ai entendu : « Quand on veut savoir la tangente en un point, ça revient à trouver la plus petite distance entre deux points … cela revient à calculer le coefficient de la droite » en accompagnant cette description des gestes évoquant une image dynamique.

Mais le professeur a rectifié  et reformuler en disant : On appelle tangente à la courbe de la fonction au point la droite passant par et de coefficient directeur Oui. Je vois. Je vois bien. Cependant, cette idée résiste à se laisser rédiger. La tangente est une droite que je  peux penser dans une position limite en « faisant comme si » la sécante était animée d’un mouvement de pivotement autour d’un point ; il arriverait un « moment » où les deux points d’intersection viendraient à se confondre, c’est-à-dire à n’en faire plus qu’un.

Difficile de dire s’il s’agit de nommer quelque chose qui, jusque là, m’échappait ou bien s’il s’agit d’un langage qui m’impose de nouvelles idées pour penser, reconnaître et utiliser.

Je me suis faite à l’idée qu’il faut non seulement se représenter la construction de la tangente en un point, mais qu’en plus il faut la rédiger, la mettre par écrit !
Traduire le dessin de la droite, c’est-à-dire construire son équation, suppose de connaître sa pente, sa direction et réclame une précision de langage.

Pour être en terrain d’entente, je m’efforces de ramasser, en une phrase ou deux, une conception longuement élaborée, une abstraction, faisant appelle à de nombreux objets mathématiques : tangente, point, distance…
Et ce besoin de synthétiser diminue la précision de l’expression de ma pensée.

C’est, sans doute, la raison de la présentation successive en nombre -> rapport -> proportionnalité -> fonction affine -> coefficient directeur vue au collège.

Le diable est dans les détails.

L’idée profonde de Parain est une idée d’honnêteté : […] « Mal nommer un objet, c’est ajouter au malheur de ce monde ».
En cours de français, nous avons étudié Les pensées de Pascal, notamment les deux infinis. Pourtant,  je  peine à dire cette petite distance.
D’autant qu’on ne calcule pas réellement la plus petite distance mais plutôt  la pente de la droite, plus précisément son coefficient directeur ( ie un vecteur directeur) nombre qui se confond avec la tangente de l’angle formé par la droite et l’axe des abscisses ( ie rapport du côté opposé et du côté adjacent).

Le prof nous a fourni un lien pour matérialiser le calcul de la tangente en différents points de la parabole

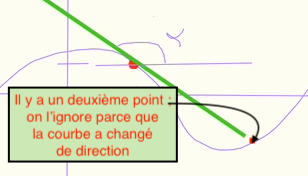Le vocabulaire qui devrait être  explicite et sans ambiguïté, s’avère douteux, une fois de plus,   avec le terme « tangente ». C’est le contexte seul qui fera choisir entre tangente de l’angle (pente) et tangente à la courbe mais surtout parce que parfois la droite tangente est aussi sécante comme dans le dessin ci-contre. Pourtant le langage mathématiques revendique la précision au moyen de définitions et de son formalisme. L’usage du français, contrairement au Globish, lui aussi, a ses qualités et ses exigences.

Ainsi le mot « tangente » ne peut pas se référer à un point puisqu’elle « caresse » la courbe.
De même distingue-t-on expression et équation :

• • L’équation est construite sur une égalité est un outil pour résoudre certains problèmes.
  • L’expression est l’une des formes sous laquelle se présente un objet mathématique,
    surtout numérique ou algébrique.

Le coefficient directeur fait-il appel à un deuxième point ?

Je dois reconnaître que je n’étais pas prête à regarder cette tangente comme cela. Changer de point de vue n’est pas facile quand on a des préjugés.

Jusqu’à présent, je pensais que les préjugés étaient un obstacle à comprendre une nouvelle idée. À l’évidence, mes préjugés sont, ici, plutôt comme une préparation à comprendre. Cela me semble comme une pré-compréhension et peut-être serait-il utile de ne pas rester fixé à l’idéal d’une connaissance dépourvue de tout préjugé. En fait il y a une histoire de l’effort de compréhension. c’est le recul du temps. la distance temporelle. qui permet de faire le tri entre les bons et les mauvais préjugés.

Préjugés

Nous avons des à priori (ex : vérifier est une perte de temps au contrôle, …) des croyances qui nous desservent,
parfois, quand elles sont erronées ou trop vague (ex : il faut mettre au même dénominateur, il faut passer de l’autre
côté…).
Se départir des a priori,
Aux appréciations sur l’énoncé ou sur moi-même, opposer une volonté de comprendre.
Être un peu soupçonneux pour éviter la perte de temps !
L’usage d’expressions approximatives dans le langage quotidien peut conduire à des erreurs de pensée.
Méfions-nous, des jolies figures de style (sommes, produits et dérivée)
Compenser par des bouffées d’air,
C’est l’ombre du doute qui conduit à la vérification ;
Nécessité d’être soupçonneuse sur ses résultats et donc … de les vérifier
L’évidence nous aveugle quand elle ne nous crève pas les yeux
Redoubler d’attention,
Raisonnement faux parce que le sens des calculs s’oublie derrière ce qui s’entend,
autrement dit la forme masque le fond.
Pour se sortir d’affaire mettre un terme aux calculs et récapituler
Notre grille de lecture est tributaire de notre point de vue ;
le propre de l’orientation est qu’elle est consciente de cette perspective ;
Enfin, une fois de plus, le problème n’est pas moi, il me reste à donner du sens à la question puisqu‘elle doit en avoir

Lire les erreurs et le corrections
Délit de sale tête d’un résultat intermédiaire,

03 Rendre présent à l’esprit

Littéral
Le sens des ‘a’ et des ‘b’ sont déterminés par la définition que tu en donnes
Les arabes nous ont légué, outre les chiffres, l’algèbre et beaucoup de théorèmes.
ET par l’usage que tu en fais.
Imaginer la raison qui a conduit à la nommer avec cet indice, m, littéral.
Manipuler des lettres comme des nombres ?
On peut s’intéresser au sens propre de « un seul point » qui se distingue de « deux points d’intersection ».
Cependant, en français, l’ordre des mots peut être perturbé et nous sommes éduqués à rétablir :
« Belle marquise, d’amour, me font mourir, vos beaux yeux ».
Les mots, même en mathématiques, réfèrent ou « en citent » d’autres. L’écriture ne peut donc être une reproduction de la
langue parlée puisque aucune (ni l’écriture, ni la langue parlée) n’existe avant l’autre.
Le concept est donc exprimé tantôt par un dessin, un mots, une expression ou une définition.
De plus il existe des signes ou des pratiques d’écriture qui participent de la signification.
« Pour définir une « analogie », objet même des proportions,
on disait et écrivait aisément au XVIe siècle en traduction fidèle du grec : A est à B comme C est à D.
A contrario du lecteur empirique, prenant le texte au pied de la lettre, le lecteur modèle possède la capacité, grâce à son encyclopédie,
de remplir les blancs au meilleur de sa connaissance et ce, en fonction de son bagage social,
encyclopédique et des conventions culturelles.
Les signes peuvent être des traces, comme des empreintes laissées par un animal,
des symptômes, des indices, des signes ostentatoires,
des répliques (comme les instances d’un vecteur) ou des inventions.

Lecture littérale. Sens figuré.
La traduction, certes, le sens figuré est à mobiliser souvent,
commencer par prendre le texte au pied de la lettre est parfois salutaire.
Le mot n’est pas la chose.
Signes, vocabulaire (suite, termes…)
Discerner dans l’énoncé les mots significatifs
Egalité et équivalence
les mathématiciens redoutent les quiproquo.
Réaliser de quoi on parle.
La reformulation volontaire conduit à rendre présent

Réaliser, ne pas passer à côté, c’est lire latéralement et non pas littéralement,

le sens propre et le sens figuré
On passe d’une idée à l’autre, par le contexte, par la similitude par la représentation graphique,
le changement d’écriture, de formulation, le point de vue ….
Changer de perspective

Faire un dessin un graphique
Réaliser par un dessin
Trraduire, faire des liens pour s’attacher les connaissances et les rendre familières.
Traduire le dessin de la droite par une équation pour être en terrain d’entente,
La fonction existe-t-elle ? Pas plus que Sherlock Holmes ou Harry Potter.
La possibilité de lier le dessin et le texte, facilite la mémorisation.

Proto épreuve

Touches voisines