Emotions

La fuite dans les idées géométrique


Dernière mise à jours 2024-01-28 par Mathilde Ohm 		Ouverture
Page suivante

Dire qu’on a « jamais vu ça » et inutile.
En revanche, partir de la question :
Qu’est-ce que « q » (initial de quotient)

*** QuickLaTeX cannot compile formula :

\begin{tabular}{lccc}
et retrouver : & $ q = \dfrac{u_{n + 1}} {u_n } $ & et notamment & q = \dfrac{u_2}{u_1} $ \\
\end{tabular}


*** Error message :
Missing $ inserted.
leading text: ... } $ & et notamment & q = \dfrac{u_2}{u_1}

Je marque beaucoup d’insistance sur cette idée de traduction (interprétation)
ce n’est pas (encore) du gâtisme de ma part.
J’ai mis longtemps à cogiter cette orientation dans la pensée (Kant, Descartes… )
je cherche, péniblement, à expliciter et présenter le plus clairement cette idée,
n’hésite pas à la discuter et, peut-être, à l’adopter.
Cela semble toujours évident à entendre, et bizarrement
on oublie de le mettre en pratique.

\left\{\begin{matrix} \text{explicitement :} & u_n = u_0 + q^n\\ \text{où} & u_0, q \text{ et } n \text { sont connus} \\ \end{matrix}\right.

Plutôt que de se lancer à la poursuite d’une manière de faire hasardeuse,
tu prends le temps d’observer….
… et tu vois que \textcolor{red}{\times q} apparaît partout et que donc on peut écrire S :

Narthex :

OK. Je m’y colle
Mathilde :[3d-flip-book mode= »fullscreen » id= »4861″][/3d-flip-book]

Narthex :

Ok. A samedi. Si tu as des questions d’ici là, n’hésites pas.

Je regarde dès que je reçois ta réponse. Tu peux les faire séparément

Mathilde :

Bonjour Jean-Jacques,
Voici un des deux exercices, je n’ai pas réussi à faire le deuxième
Pourriez vous jeter un coup d’œil

Narthex :

Remarquablement bien présenté. Je vais lire. Merci
Excellent. Je te donne ma rédaction qui est très voisine de la tienne.

Souhaites-tu tenter de résoudre le premier ou veux-tu le corrigé ?

Mathilde :

Je préfère avoir le corrigé merci

Narthex :

Entendu, le voilà :

[3d-flip-book mode= »fullscreen » id= »4667″][/3d-flip-book]

Je mets en pièce jointe la synthèse pour mémoire

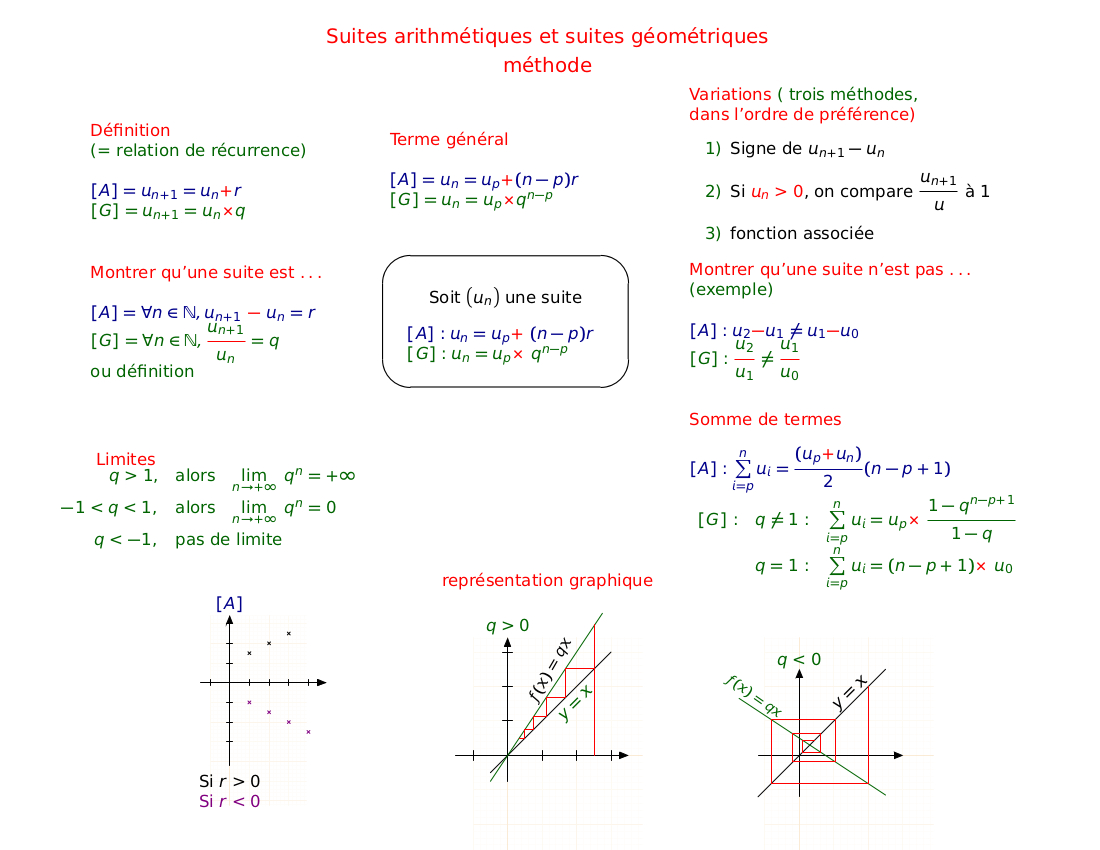
Et pour suivre un exercice mêlant suite géométrique et trinôme :(u_n) est une suite géométrique à termes non nuls, de raison s\neq 1 telle que :
5u_2 = 7u_i - 2 u_0

  • Déterminer la rasion q de la suite (u_n)
  • On donne u_0 = 6.25, calculer u_4

J’en ai d’autres si celui-ci te semble trop simple.

Connais-tu l’« effet latent » ? Il se résume ainsi :
« On apprend à nager en hiver et à patiner en été »
parce que pendant que tu fais ton cours d’anglais,
ton cerveau continue à chercher la solution du problème de math
et quand tu t’y remets, la solution ne tarde pas à s’imposer.

Bravo pour cette démonstration.
C’est loin d’être trivial.
Et cela renforce l’idée d’effet latent, d’une part,
et, d’autre part nous amène à cette question :

Emotions
 Ouverture
Page suivante