07. Un mot peut
en cacher un autre
Coccinelles

Contrat plus ou moins implicite


Dernière mise à jours 2025-06-19 par Mathilde Ohm 		09. C’est à quel sujet ?
Page suivante

Novembre (semaine 45)

Du Python, de l’analyse, du réel, des invariants … quelques notes à propos de ce matin.

Qu’apporte l’habillage du problème dans le style « math appliquées » si ce n’est que pour estomper le caractère abstrait de la question au profit de l’illusion d’une proximité avec la réalité. (ex : Un médicament contre la douleur ….).
Cela peut induire des idées parasites à la résolution de l’exercice, comme les moutons qu’on extrapole tondus des deux côtés.
Dans l’exercice d’aujourd’hui, le poids n’est pas un élément pertinent …

Quel est le contrat ?

Ce que j’aime bien avec P’ti Roy c’est la clarté de ses cours. Pourtant il arrive les mains vides à l’exception  d’un petit bout de papier de la taille d’un ticket de bus et pourtant il laisse un tableau bien ordonné affichant tous les éléments de la leçon. À l’évidence savait ce qu’il laisserait à voir.

Sauf rare exception, toutes les informations nécessaires sont présentes dans l’énoncé :
il ne doit pas en manquer et aucune n’est superflue.
C’est important de garder ce contrat en tête pour ne pas être hors sujet.
Dans le contexte de la classe ou de l’examen, le problème posé prend en considération l’élève auquel il est destiné
et, donc, ne comporte ni piège, ni difficulté insurmontable.
Enfin, rappelons-nous, que les exercices ont (presque) toujours l’intention d’apprendre quelque chose.

Dans un effort pour comprendre on peut rendre, en quelque sorte, justice à l’auteur,
c’est-à-dire faire l’hypothèse que le rédacteur a voulu dire quelque chose de sensé et a voulu être compris.
Cette attitude, érigée en principe, s’oppose à l’idée de secret occulte ou de rébus — fin de l’alchimie, par exemple.

Lorsque l’on exécute un programme (en Python, ou autre), l’ordinateur commence par une première vérification
et vérifie que les expressions sont bien formées. Les concepteurs du langage ont prévu des messages d’erreur
indiquant l’utilisation de mots inappropriés ( ex : intervalle = L [] ) ou des messages explicitant l’infraction à la syntaxe
(ex la ligne commençant par un test, if, while … doit être suivie d’un bloc indenté.) et donc le système commence par soupçonner la présence d’une erreur triviale.

Lire les messages d’erreur et un gain de temps !

De même est-il prudent de s’assurer, dans la rédaction, des précautions prises , le soupçon diminue l’incertitude 80)

L’interprétation du résultat tient compte de la formulation de l’énoncé
2) Exécuter le programme Que contient la liste intervalle à la fin du programme ? Interpréter le résultat.
On obtient la liste [1, 2, 3, 4, 5].
Le médicament est actif entre 0 et 5h (5ème heure incluse). Il faut administrer à nouveau le médicament au bout de 6h à partir de x=5).

La deuxième partie de l’exercice concerne la compréhension du modèle proposé :
C(t) = t^3 -12t^2 +36t + 1

Il est toujours utile de se faire une image mentale de la fonction. Pour l’instant une esquisse est bienvenue,
« C’est un polynôme de degré 3, donc il y peut y avoir 2 extremum, le coefficient du degré le plus élevé étant positif, la fonction commence par croître » Bravo !

On peut couper court est calculer le nombre dérivé au moyen de la fonction dérivée :

f'(2)=-3

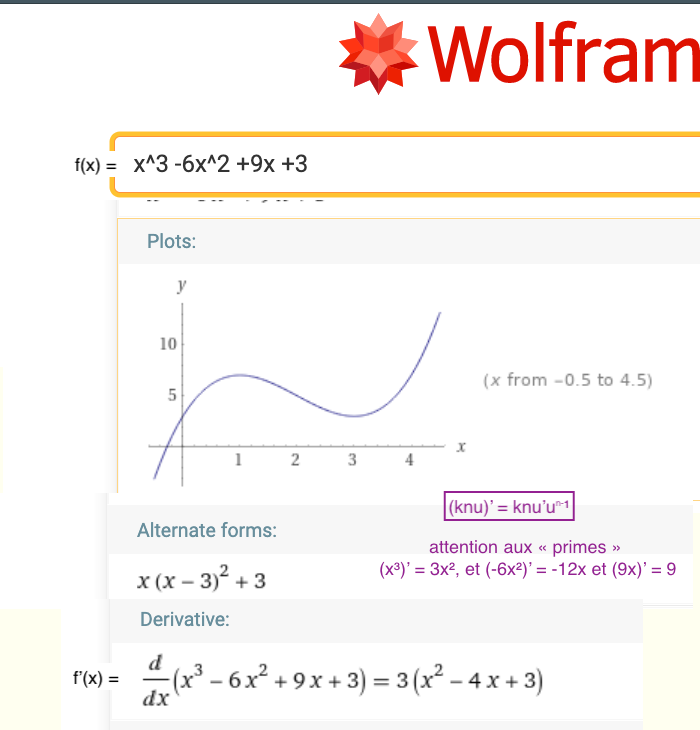
Si l’on demande de Restituer de façon Organisée cette Connaissance (ROC)
il conviendrait de faire la calcul :

    \[ \lim_{x\rightarrow 0} \dfrac{(h+2)^2 - 9(h+2)^2 + 9(h+2) - (h^3 -6 \times 2^2 + 9 \times 2 +3) +3}{h} \]

    \[\Downarrow \]

    \[ h^2 -3 \]

Ce qui nous prendra d’autant plus de temps qu’il faudra recommencer
pour chaque tangente en un autre point d’abscisse autre que 2.
L’avantage de la fonction dérivée f'(x) est de minimiser les risques d’erreurs.

Cela dit, la difficulté tient plutôt à cette question de limite et de h.
La valeur finale de h est connue : c’est 0 (zéro) ce n’est donc pas la distance que l’on calcule.

Notre but est de déterminer la valeur finale du rapport \dfrac{f(a+h) -f(a)}{h}

Les formes et les figures dans les expressions
L’abréviation est l’une des formes prépondérantes (10³ pour 1000, …)
La définition, tantôt  explicite et tantôt implicite, est systématique  p233 normative (dérivable), descriptive (parallélogramme), condensation (vecteur) p283
La citation, marque l’appartenance à une communauté, (d’après Pythagore, …)
L’énallage de la personne pour associer l’élève (Nous allons montrer que …)
L’incompatibilité (p264) et le tiers exclu (en mathématiques). Quid de ceux qui vivent un conflit ?

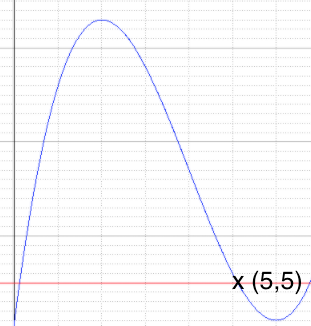
Pour préciser cette représentation, l’étude des variations de la fonction C(t)
est obtenue au moyen de la fonction dérivée :
Rappel :(\textcolor{purple}{k}\textcolor{green}{u}^{\textcolor{red}{n}})' = \textcolor{purple}{k}\textcolor{red}{n}u'\textcolor{green}{u}^{n-1}, et la dérivée d’une somme est la somme des dérivées.

C'(t) = 3t^2 -24t +36

et synthétisée par le tableau

L’une des difficultés qui se profile à l’horizon des semaines prochaines,
sera de répondre à la question « La fonction est-elle dérivable ? »

Pour y comprendre quelque chose, il est intéressant de poser la question
en utilisant une expression sous forme négative :
« Qu’est-ce que fonction qui n’est pas dérivable ? »

En reprenant la définition :

La fonction dérivée de ƒ, notée f',

  1. est la fonction qui, à chaque \displaystyle x\in I,
  2. associe le nombre dérivé \displaystyle f'(x) de ƒ en x.

 

  1. Donc, hors du domaine de définition, pas de fonction dérivée :

    Exemple f(x) = \frac{1}{x}, x \in \quad ]-\inf; 0[ \cup ]0;\inf[
    il y a un « trou  en zéro », donc on ne peut pas dériver.
  2. S’il existe 2 nombres dérivés pour une même valeur de l’antécédent x
    il y a indétermination et on considère que la fonction n’est pas dérivable.
    Exemple f(x) = |x|, n’est pas dérivable pour x = 0

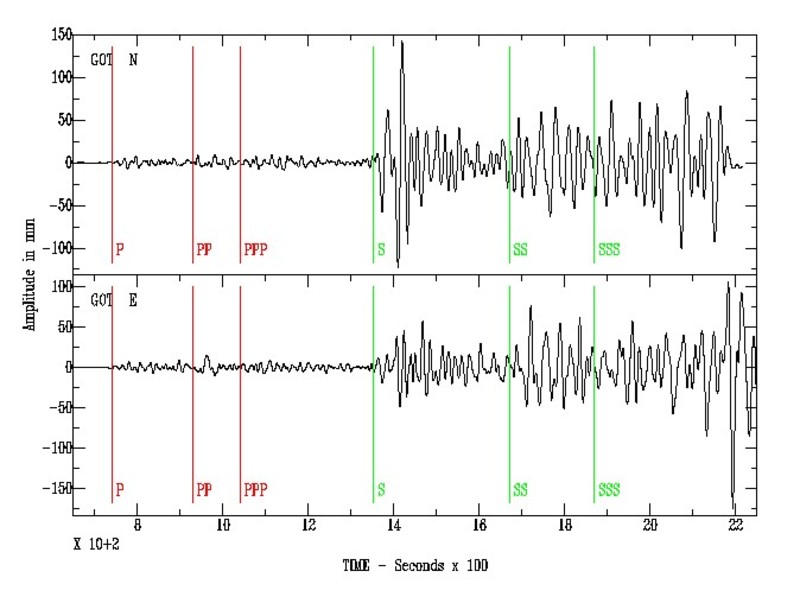
Le fonction semble continue, cependant

  • si que l’on s’approche de gauche ou de droite, le nombre dérivé est le même,
    alors la fonction est dérivable en ce point
  • si en s’approchant de gauche, le nombre dérivé différé de celui obtenu en s’approchant par la droite
    alors la fonction n’est pas dérivable en ce point.

Par exemple :

\begin{tabular}{cccccl} Soit la fonction $f$ : & $\mathbb{R} \longrightarrow \mathbb{R}$ \\ & $x \mapsto f(x) $ & $=$ & $\dfrac{2x-8}{x-3}$ & si & $x \in ]-\inf ; 2[$ \\ & & $=$ & $-x^2 +6x -4$ & si & $x \in ]2;5[$ \\ & & $=$ & $\dfrac{2x-8}{x-3}$ & si & $x \in ]5 ; \inf [$ \\ & et $f(2)$ & $=$ & $4$ \\ & et $f(5)$ & $=$ & $1$ \\ On a donc $\mathcal{D}_f = \mathbb{R} $\\ \end{tabular}
Ça se voit, certes, encore fallait-il le prouver par calcul.

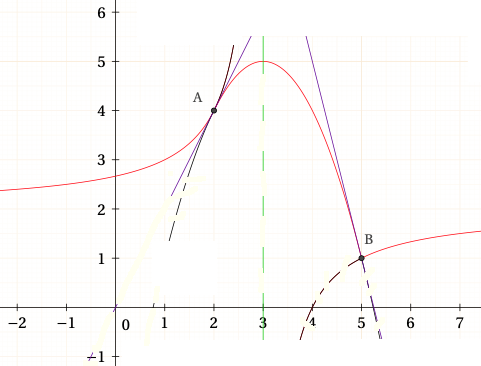
Plutôt que de se précipiter dans les calculs,
commençons par mettre en relation certains éléments de l’énoncé :
La fonction rationnelle, avec son dénominateur qui s’annule en 3,
aurait dû conduire à exclure le réel « 3 » des antécédents pourtant l’énoncé indique \mathcal{D}_f = \mathbb{R} et non pas \mathcal{D}_f = \mathbb{R}\backslash\left\{3\right\}
On constate que x=3 appartient à l’intervalle ]2;5[
ce qui nous rappelle qu’il convient de partir de l’idée que l’énoncé est supposé cohérent.

Le coefficient de x^2 est négatif, ce qui confirme l’orientation de la parabole,
qui n’est définie qu’entre A(2; 4) et B(5;1), ne s’annule pas.
Inutile de calculer les racines du polynôme. Ce serait du temps perdu.

Dans le plan systématique de la fonction, il nous faut
répondre aux questions : « La fonction est-elle continue ? »
« La fonction est-elle dérivable ? »
Pour l’instant nous n’examinons que les deux A et B.

S’il est vrai que l’application Zoom ne facilite pas les calculs en ligne
comportant des fractions, il est, pourtant, préférable de garder la trace
des calculs afin de pouvoir revenir déloger une erreur éventuelle.
Être un peu soupçonneux pour éviter la perte de temps !

La fonction est continue bien que partout dérivable sauf pour x=5, puisque pour x=5,
il y a deux nombres dérivés.
Mais on sait que la fonction est est définie pour x=5, donc…

Par ailleurs, l’usage d’expressions approximatives dans le langage quotidien
peut conduire à des erreurs de pensée :
dans l’équation de la droite f(t) = mt+p ou f(x) = mx +p, t et x ne sont pas des inconnues
ce sont des variables.

Au cours de la simplification \dfrac{\cancel{\textcolor{red}{h}}(-h-4)}{\cancel{\textcolor{red}{h}}} les « h » ne s’annulent pas ! d’autant plus que l’on cherche \lim_{h \rightarrow 0} T(h) = \lim_{h \rightarrow 0} -h -4 ce qui se lit :
limite de moins h moins quatre quand h tend vers zéro et l’on pourrait penser que h va s’annuler. Ce qui n’est pas le cas.
Sinon impossible de simplifier en divisant par h !

Mon père disait : « Tu serres et tu t’arrêtes un quart de tour avant que ça casse ».

Je mets la rédaction en pièce jointe.
Rédiger de cette façon favorise une note maximale Ne varietur

Parvenir à cette étape ultime de la compréhension, suppose d’avoir accepté le contrat souvent implicite. Le texte mathématiques  tient pour acquis qu’il est compréhensible par l’élève, qu’il n’évoque que des objets ou des notions connues, que la formulation est sans équivoque et que la bonne volonté du lecteur est acquise de sorte que toute interprétation incohérente sera rejetée. À cette fin, l’auteur est sensé fournir toutes les information requises,  n’affirmer que ce qu’il croit être vrai,  ne dire que ce qui est pertinent,  et être clair, sans ambiguïté. Ajoutons, la clarté de l’énoncé,  l’élégance de la forme,  adéquation, c’est-à-dire, éviter les hors sujets ou les digressions.

07. Un mot peut
en cacher un autre
Coccinelles
 09. C’est à quel sujet ?
Page suivante