03. Le bon sens des mots

Le bon sens des mots


Dernière mise à jours 2024-04-11 par Mathilde Ohm 		04. Et en suite ….
Page suivante

Énoncé

Définition : deux rectangles sont de même forme lorsque les rapports longueur/largeur sont égaux. (C’est le cas entre un négatif de 24 \times 36 et une photo sur papier photo 10 \times 15  car on a : \dfrac{36}{24} = \dfrac{15}{10}.

Une feuille de format A0  a une aire de 1m^2  exactement.

Lorsque l’on coupe cette feuille au milieu de la longueur, on obtient deux feuilles de format A1. Lorsque l’on coupe une feuille de format A1 au milieu de la longueur, on obtient deux feuilles de format A2, et ainsi de suite (voir figure ci-contre).

Rendered by QuickLaTeX.com

1. On note L la longueur et 1 la largeur du format A0, en mètre. Prouver que l est l’inverse de L.
2. On note a le rapport des dimensions du format A0 :a = \dfrac{L}{l}.
Exprimer a en fonction de L.
3. On note b le rapport des dimensions du format A1. Exprimer b en fonction de L puis en fonction de a.
4. Sachant que le rectangle de format A1 est de même forme que le rectangle de format A0 (voir définition ci-dessus), calculer la valeur exacte de a.
5. Déduire de la question précédente le calcul de L (arrondir le résultat à 10^{-5} près). Calculer ensuite la largeur l. Quelles sont les dimensions du format A0 en cm ?
6. D’après le découpage ci-contre, quel est le nombre de feuilles A4 que l’on obtient dans une feuille de format A0 ? Calculer les dimensions d’une feuille de format A4 en cm à 1 mm près.

À la première question, les mots longueur et largeur me  semblaient familiers et pourtant je ne comprenais pas.   Comment la largeur pouvait-elle  être l’inverse de la longueur ? Non pas que j’ignore le sens du mot « inverse », je sais même le distinguer du mot « opposé », mais comment établir par calcul que l = \dfrac{1}{L} ?
J’ai demandé de l’aide à Monsieur Narthex par sms. Pour lui, cela était écrit dans l’énoncé, et il m’a poussée à relire jusqu’à déterminer l’aire de la feuille de format A0. C’est ainsi que j’ai fini par écrire qu’un mètre carré est égal au produit de la largeur par la longueur : l \times L =1, comme au collège et ensuite d’écrire \dfrac{ l \times L}{L} = \dfrac{1}{L}, puisque je peux diviser chaque membre de l’égalité par le même nombre.  Ensuite  il est possible de  simplifier \dfrac{ l \times \color{red}\cancel{\color{black}{L}}}{\color{red}\cancel{\color{black}{L}}} = \dfrac{1}{L} et de répondre \boxed{l=\dfrac{1}{L}}. Et après ?

La deuxième question me semblait tout aussi obscure : pourquoi,  diable, introduire la lettre « a = \dfrac{L}{l} », jusqu’à ce que je réalise pouvoir remplacer l, grâce  à la première question,   par \dfrac{1}{L} dans a = \dfrac{L}{\color{purple}{l}}  ce qui devient a = \dfrac{L}{\color{purple}{\frac{1}{L}}} et donc, puisque « pour diviser par une fraction, on multiplie paf l’inverse » on obtient \boxed{a = L^2}.

La troisième question semblait me faire tourner en rond, puisque après avoir calculer a en fonction de L à la question précédente, il me fallait maintenant calculer L en fonction de a. Mais là, surprise,a = L^2 quad \Longrightarrow L = \sqrt{a}, ce qui n’avance pas franchement à grand chose.
Monsieur Narthex m’a fait remarquer que j’avais omis de répondre à la première partie de cette troisième question : « On note b le rapport des dimensions du format A1. Exprimer b en fonction de L…».
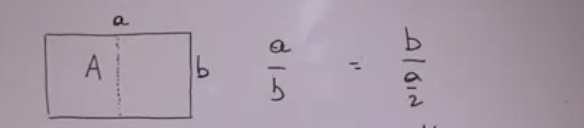
Je me suis résignée à écrire \dfrac{\mathrm{largeur}}{\mathrm{Longueur}} = \dfrac{a}{b}.

Ce à quoi, Monsieur Narthex m’a répondu :

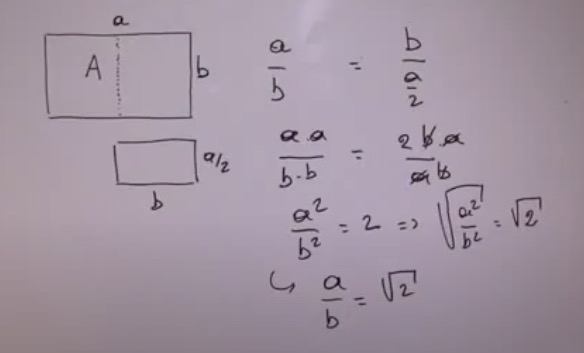
Que sont ces a et b que tu mets dans ton égalité ? Ce serait bien que tu dises ce à quoi tu penses ? Il me semble que tu désignes des objets sans utiliser des mots qui « clarifient», qui « différencient » afin « d'élucider ».
Certains mots peuvent être amphibologiques, c’est-à-dire ambigus, propres à nous jeter dans la confusion. Ici ces mots sont : largeur, longueur…
Pour s’y retrouver, il convient d’être plus précis. Largeur DE QUOI ! Longueur DE QUOI ? Le brouillard devrait se lever 80)

. . . et, oui, le brouillard s’est dissipé quand j’ai compris que a est le double de b sur mon dessin, puisque la feuille est coupée en deux moitiés égales.

J’ai continué à tâtonner vers la sortie que j’espérai à la fin des calculs, jusqu’à établir un rapport égal à \sqrt{2}.

Cela illustre bien que le sens des ‘a’ et des ‘b’ sont déterminés par la définition que tu en donnes ET par l’usage que tu en fais. Il n’y a aucun lien direct entre ‘a’ et longueur. Pas plus qu’il y a un lien direct entre ‘chaise’ et l’objet où tu es posée. Relis Lewis Caroll : En effet, tu confonds a et b qui, dans l'énoncé, désignent des rapports avec les dimensions de la feuille. Si bien que tu sembles avoir trouvé la bonne valeur du rapport par un heureux hasard.
De plus cela ne répond pas à la dernière question Calculer les dimensions d’une feuille de format A4 en cm à 1 mm près.


Monsieur Narthex m’a proposé de rencontrer Madame Émilie du Châtelet qui a contribué à diffuser en France l’œuvre physique de Leibniz ; Madame du Châtelet, après avoir écouté mes questions, m’a conseillé d’évaluer les ressources nécessaires pour résoudre un problème, de réfléchir à leur disponibilité ou à la manière de les acquérir, de suivre ma progression en prenant bien des notes, de reconnaître les moments où je suis bloquée, d’identifier les possibles causes du blocage, d’élaborer des stratégies pour y remédier,

d’évaluer l’effort requis pour les mettre en œuvre, et de tirer des leçons des échecs précédents, c’est-à-dire de corriger ma perception du travail et en d’améliorer l’utilisation.

Ouf. J’ai réussi à mémoriser les indications, mais vais-je savoir faire ça ? D’ailleurs, est-ce une méthode spécialisée que je puisse acquérir, ou au contraire est-ce une capacité utile à tout comme la mémoire et dont mon cerveau serait, ou non, pourvu ?

03. Le bon sens des mots
 04. Et en suite ….
Page suivante