Plus ou moinsDernière mise à jours 2024-01-28 par Mathilde Ohm |
La suite ne s’est pas fait attendre : « Addition des nombres relatifs »
Et là il y a une règle à respecter !
J’ai écrit « La suite ne s’est pas fait attendre », parce que mon professeur de français nous a appris la règle. Elle a dit que c’est une erreur fréquente que de vouloir suivre les règles générales d’accord du participe passé pour le verbe « faire » et d’écrire « La suite ne s’est pas faite attendre » au lieu de « La suite ne s’est pas fait attendre ».
Et elle a ajouté :
Rien que de très logique, finalement, dans cette règle : le complément d’objet direct avec lequel on serait – à tort ! – tenté d’accorder le participe sous prétexte qu’il le précède n’a rien à voir avec ce dernier, mais avec le verbe à l’infinitif qui suit. Il est donc normal qu’il ne soit d’aucune influence sur l’accord dudit participe…
Il m’a fallut un certain temps pour comprendre !
Mais revenons aux nombres relatifs. Est-ce logique aussi ?
Voici la règle de Monsieur Bozons notre prof de maths de cette année :
J’ai retenu que les nombres relatifs « c’est comme » les dates, les degrés et les ascenseurs. Je ne me vois ni ajouter des dates ni ajouter des degrés, pourtant Monsieur Bozons nous a donné des exercices 
:
Et pour couronner le tout, une multitude de questions du genre :
À première vue ces calculs ne ressemblent pas au calcul de la mort d’Archimède ou à celui de la différence des températures sur la lune. De plus j’ai hésité devant l’alignement des énoncés et des corrections : à droite de la question « B » j’ai fini par comprendre qu’il s’agissait de la réponse à la question « A » et encore à droite la réponse à la question « C ». Tandis qu’à droite de la question « D » on trouve la réponse à la question « B » puis la réponse à la question « D ». Cela fait un peu désordre, mais j’ai fini par m’habituer.
Pour le prof, cela doit lui être évident, tellement il est habitué ; moi il m’a fallu chercher et je ne sais même plus comment j’ai fini par trouver. La prochaine fois, j’essayerai de noter comment j’ai cherché et comment j’ai compris avoir trouvé. Enfin
, si j’y pense.
Mais, bon. C’est du détail. Le plus important serait de découvrir ce que cela veut dire ?
|
Je me souviens que notre prof nous a raconté l’histoire de la « pierre de rosette » ; vous savez, cette stèle égyptienne gravée de trois versions d’un même texte qui aurait permis le déchiffrement des hiéroglyphes par |
 |
Et voilà que Monsieur Bozons nous propose un jeu avec des jetons noirs ● et blancs ○.
Il nous a montré une vidéo :
que je résume.
Il précise qu’un jeton blanc sera représenté par « + » et un jeton noir par un « – »
|
1) Additionner est un jeu d’enfant : |
 |
|
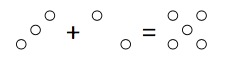Ce que tout le monde écrit : |
(+3) + (+2) = (+5) |
|
S’il s’agit de jetons noirs : |
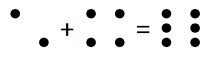
(-2) + (-4) = (-6)
|
Et, puisque un jeton noir et un jeton blanc s’annulent :
 |
|
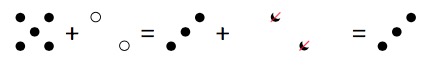| ce que l’on peur écrire : | (-5) + (+2) = (-3) + (-2) + (+2) = (-3) |
| 2) Soustraire n’est pas plus sorcier, |  |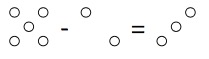
| Et on écrit : | (+5) – (+2) = (+3) |
| S’il s’agit de jetons noirs : |  (-6) – (-4) = (-2) |
|
3) Surprise : on peut soustraire plus jetons d’une couleur qu’il n’y en a |
 |
|
Et on écrit : |
(+2) – (+5) =(+2) – (+5) +(+3)+(-3)=(-3) |
|
Et même : |
(+2) – (-3) =(+2) – (-3) +(+3)+(-3)=(+5) |
La comparaison avec les jetons m’a semblée parlante et j’ai couru la montrer à Papa. « Oui, m’a-t-il dit, c’est convaincant. Mais attention : comparaison n’est pas raison. Soit prudente quand tu fais des maths appliqués.
Imagine-toi assise sur un banc public. Tu vois deux personnes qui rentrent dans une maison. Puis, après quelques temps, tu vois trois personnes ressortir de la maison. Crois-tu que si quelqu’un rentre dans la maison, alors la maison sera vide…
Pourtant, cela pourrait s’écrire : (+2) – (+3) + (+1) = 0 »
